在我们有限的认知中,似乎也就只有LGU的学生每天都会遇到这样一个问题:去饭堂,走哪边?每当看到一左一右两个路径,有时甚至恨不得从中间翻过去。除了在心里对校园规划心存怨念之外,两条路,究竟走哪条?生活还得继续。数学派对这个问题进行了研究,试图用理性解决这个世纪问题。
想看剧透?点这里。
同时,数学派还提供了一个Python脚本让大家根据自己的身体参数等进行计算最优路线。
我们分为平面行走、爬坡、爬楼梯三个模型讨论,并附加关于太阳光照的考虑。
平面行走模型
问题简述:人行走时的能量主要用于维持正常的生理需求和行走的能量损耗,但究竟行走需要消耗多少能量 ?那些能量又流向何处呢?本文将在平面行走的情况下对行走的能量损耗进行研究,希冀能够得出结论 。(其他几种情况将在以后的模型中加以讨论)
问题分析: 人行走的能量损耗主要流向两个方向,一个是用于人体重心的变化,另一个是用于提供腿部动能。因此,本文将主要对这两个方面展开分析。
假设:
- 人在行走时所做的功,完全由两部分组成:提高人体重心的势能,两条腿运动的动能;
- 人行走过程视为腿绕腰部的转动;
- 忽略穿戴影响,地面平坦,干燥;
- 设定参数: 人的体重- – – M(kg); 人的腿重—m(kg);
人的腿长—l(m); 行走速度—v(m/s); 步长—x(m); 总步数—n
三、建立模型
1.人体重心提高所需的势能
令人体重心提高的幅度为h,则有:
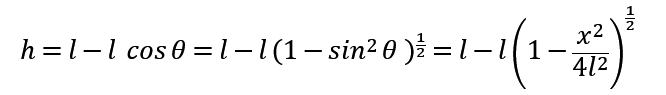
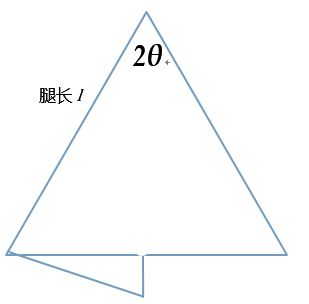
由动能与势能的关系可知,单位时间内重心抬高h所需的势能为:
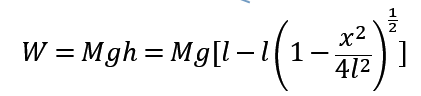
此式子即为走一步所产生的势能,则走了 n 步有:
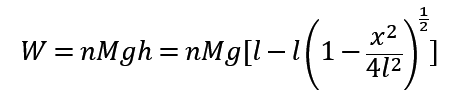
2.双腿运动所需要的动能:
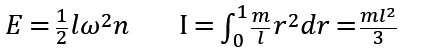
ω为角速度,I为转动惯量
由动能定理得:
则有
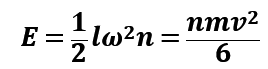
则人在走路时所作的总功:
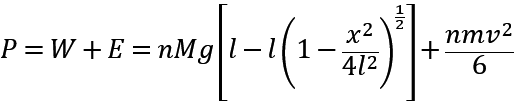
因为![]() ,所以:
,所以:
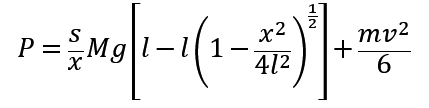
误差分析:
本模型忽略了风力等自然因素,运动模型高度理想化,忽略了人体竖直方向上 的动能,而且,运动过程中质心的位置和速度也是变化的,因此,本模型与实际情况有误 差,仅供参考。
References:
1. 《人行走时最小功模型》;
2. 《人行走最佳速度模型》;
3. 《姜启源,谢金星,叶俊主编.数学模型(第三版).北京:高等教育出版社.03.21- 22
爬坡模型
问题简述:
人行走时的能量主要用于维持正常的生理需求和行走的能量损耗,但究竟行走需要消耗多少能量?那些能量又流向何处呢?本文将在坡面行走的情况下对行走的能量损耗进行研究,希冀能够得出结论 。(其他几种情况将在以后的模型中加以讨论)
问题分析:人行走的能量损耗主要流向两个方向,一个是用于人体重心的变化,另一个是用于提供腿部动能。而在爬坡过程中,与其他情况显著不同的就是对于重力势能变化的分析。因此,本文将主要对这两个方面展开分析。
假设:
- 人在行走时所做的功,由两部分组成,提高人体重心的势能,两条腿运动的动能;
- 人行走过程视为腿绕腰部的转动;
- 忽略穿戴影响,地面平坦,干燥;
- 设定参数:人的体重—M(kg);人的单条腿重—m(kg); 人的腿长—l(m);行走速度—(m/s); 总步数—n 步长—x(沿斜面) 斜面倾角—theta
- 非承重腿于斜面最小夹角—alpha 总路程—s(m)
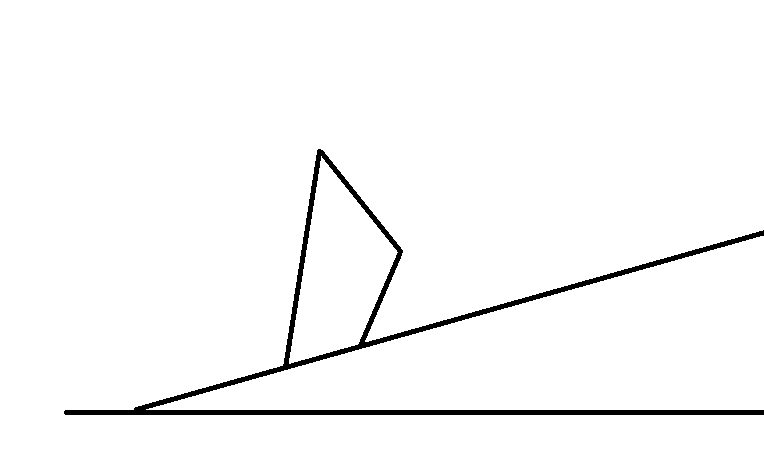
建立模型: 在斜面类行走模型中,对于行走的方式一直有所争议,本文不予讨论行走姿势的问题,而是从能量角度,寻找能量的差值。
Part 1 腿部的分析
假设腿为一均匀细杆,则双腿运动所需要的动能:
由动能定理得:
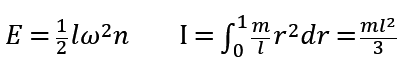
ω为角速度,I为转动惯量
则有
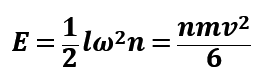
Part2 重力势能分析:我们需要找到一步的行走中最高的一点。应该注意到,在如下图所示的一个周期内,原承重腿始终没有发生变化,分析可知当处于如图所示姿势时为重力势能最高点,即重力势能做负功的结束点,因此,可以知道,重力势能负功之和为黑色起始姿势与蓝色姿势的差值,可以算得:
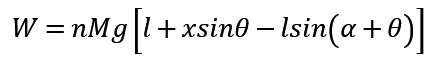
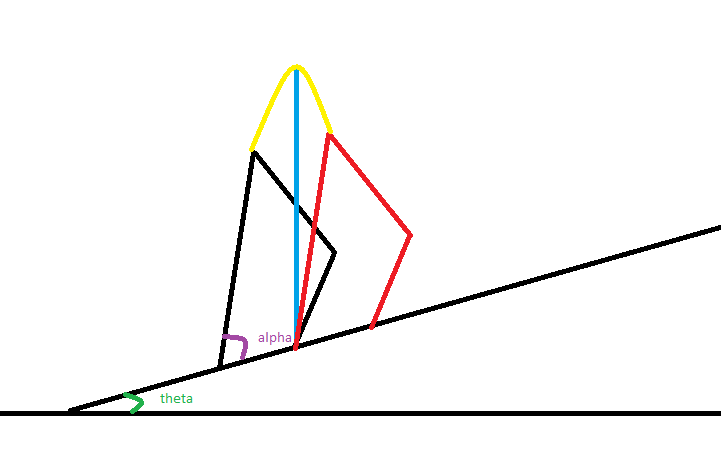
综上所诉:
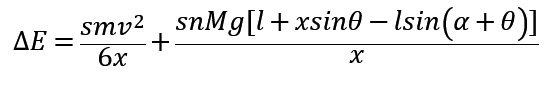
误差分析
本模型忽略了风力等自然因素,运动模型高度理想化,忽略了诸如竖直方向上动能,运动阻力等能量损耗,对于腿部运动的角速度分析过于简单,且运动过程中质心的位置和速度也是变 化的,因此,本模型与实际情况有误差,仅供参考。
References:
1. 《人行走时最小功模型》;
2. 《人行走最佳速度模型》;
3. 《坡度与运动》;
4. 姜启源,谢金星,叶俊主编.数学模型(第三版).北京:高等教育出版 社.03.21- 22
爬楼梯的能量模型
主题:本文是在人体平面运动的基础上分析人体爬楼梯过程中的能量流动。
问题分析:理想状态下的爬楼梯过程中,可分为三个过程:
- 平地→第一阶楼梯(如图所示的准备阶段);
- 楼梯→楼梯;
- 最后一阶楼梯→平地。
过程2可分为升高和下降两个过程,而过程1和过程3 可视为过程2的一部分,人体做工区别几乎为0 。因此,本文将仅对过程2进行分析;
模型假设
(笔者能力有限,故本模型仅对向上爬楼梯的过程分析)
1. 人体质量:M(kg),单条腿质量 m;
2. 重力加速度:g(m/s2)
3. 腿部长度:l(m);
4. 人体质心速度:V(m/s),竖直方向上最大速度为 u(m/s),由于考虑向上的速度变化时,腿部运动较为复杂,而根据能量守恒定律,该动能最终又大部分转化成重力势能(少部分阻力消耗),因而本文及其他文章均将 u 的动能全部合并到重力势能中,不单独讨论;
5. 台阶高度:h(m);
6. 台阶长度:r(m);
7. 经观察,本问题所涉及的我校台阶均可以每台阶跨一步,故假设行走者每台阶跨一步,每一步 迈出同样的距离(台阶宽),并且连续前进;
8. 爬楼梯过程中人体上身水平速度趋于稳定,故本文忽略稳定状态时人体水平速度变化,假设该 过程中人体质心相对于人体的位置恒定。
9. 运动过程中非承重腿与水平台阶面最小夹角为θ;
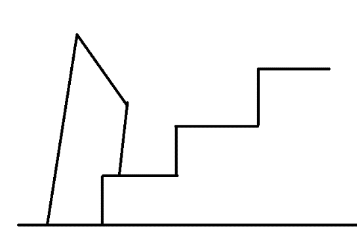
模型构建:以一个台阶为一个周期,对于第二阶段,我们有:
Part1: 上身运动
在人体爬楼梯的过程中,分析可知,当人体直立时重心最高,而当 theta 最小时,重心最 低,故而,我们可以得到:
![]()
化简可得:
![]()
Part2: 腿部运动:
假设腿为一均匀细杆,则双腿运动所需要的动能主要为转动所需的动能,假设人腿为一刚体,根据刚体力学和动能定理,我们分析可以得到:
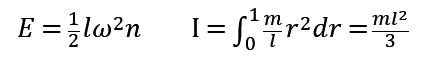
ω为角速度,I为转动惯量
则有
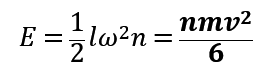
误差分析:
本模型忽略了风力等自然因素,运动模型高度理想化,运动过程中质心的位置和速度也是变化的,运动过程也忽略了细节之处,如:每次的落点不一定相同 。因此,本模型与实际情况有一些误差,仅供参考。
References:
1. 《人行走时最小功模型》;
2. 《人行走最佳速度模型》;
3. 《楼梯设计与力学模型》;
4. 姜启源,谢金星,叶俊主编.数学模型(第三版).北京:高等教育出版 社.03.21- 22
根据以上三个模型,我们编写了一段代码(python)计算步数、时间和所消耗能量,使用的是默认数据,同学们可以根据自身情况修改数据。详情见附件。基于此数据,我们计算的结果是:图中路径 2 路程最短、用时最少且消耗能量最少。
关于太阳光照的考虑
基于上述,现在来考虑太阳光照的影响(此处仅讨论晴天的情况),这时我们
主要观察正午时段(设定为 12:00整;此时段前往乐天楼的人较多且日照较强)。假定我们考虑的时期为4月中旬至 7 月下旬(约暑课结束)。从 4 月中旬到 6 月 23 日前 后,即夏至日之前,太阳直射点应位于 23°26′N 以南。由于深圳纬度(约为 22°30′)和北回归线纬度非常接近,且对下文结论影响不大,所以此处将深圳看作与北回归线 同纬度。根据太阳视运动模型,这段时间内日出东北,日落西北,而正午时太阳位于正南。
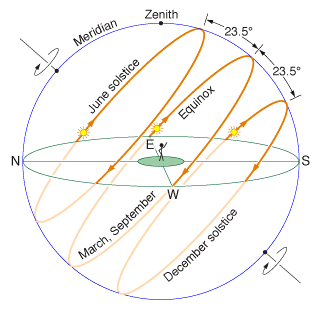
然而,这样的计算是基于平均太阳日长度(Mean solar time),即全年太阳日均值:23 小时 56 分 4 秒。而真太阳长度(Apparent solar time)在时刻变化,也影响着正午时太阳的方位。这是我们需要考虑这段时间的真太阳日长度:
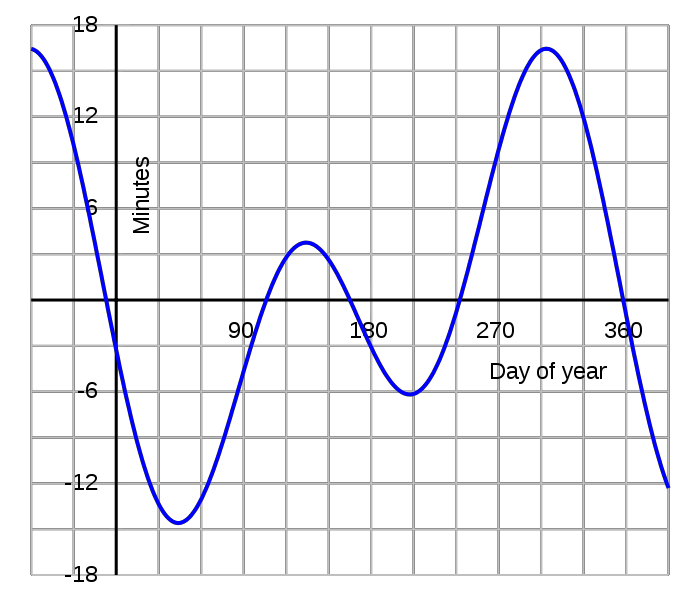
由图可知,从 4 月中旬到 5 月中旬真太阳日长度大于均值,5 月中旬等于均值,从 5 月中旬到 7 月下旬小于均值。现在我们分为 3 个阶段讨论:4 月中旬到 5 月中旬,5 月中旬到 6 月 23 日前后,6 月 23 日前后到 7 月下旬。
4 月中旬到 5 月中旬:
此时段内,真太阳日长度大于均值。因为太阳日是由太阳重复出现在同一观测 位置的周期长度来定义的,所以我们可以理解为此时太阳需要更长时间来到达天穹中同一观测位置,即此时在地球上观测太阳的运动会相对均值时更慢。那么在正午时, 太阳本应到达正南,但受到真太阳日时间变化的影响,此时应位于理想位置偏东(因为太阳在地球上观测为自东向西运动),所以这个时段正午太阳方位应为东南方。根据这个结论,理论上来说,选择校园东侧的路径前往乐天楼,会一定程度上享受到知 新楼前广场东侧的树荫和诚道楼的阴影,再加上志仁楼一楼的全阴路径,会达到一定的遮阳效果。当然,选择校园西侧路径到达乐天楼,则可以利用路径5东侧的少量树荫遮阳。
5月中旬到6月23日前后:
此时段内,真太阳日长度小于均值。与我们讨论的上一个时段同理,正午时太阳应早已到达正南位置并偏西运动了一定距离,所以正午太阳方位应为西南方。根据这个结论,理论上来说,路径5的树荫(包括齐贤楼所在山丘上的树的影响)遮阳效果不会太理想,因为此路径基本为西南--东北走向。而在校园东侧的路径则可以利用志仁楼的阴影。虽然此时诚道楼已不起遮阳作用,但知新楼前广场东侧的树荫还是可以利用的。
6月23日到7月下旬:
此时段内,太阳从北回归线向南移动,真太阳日长度也小于均值,所以正午太阳方位的变化路径会与上一种情况基本相反,但正午太阳方位还是位于西南,因此结论和上一种情况相同。
总结来说,从4月中旬到5月中旬,校园东侧的路径和西侧的路经5会有一定遮阳效果;从5月中旬到7月下旬,校园东侧路的遮阳效果会强于西侧。
图片来源:
- The CDO (Campus Development Office) of CUHKSZ.
- https://www.washingtonpost.com/news/capital-weather-gang/wp/2013/06/20/summer-solstice-2013-northern-hemispheres-longest-day-highest-sun-of-the-year/
- https://en.wikipedia.org/wiki/Solar_time
关于 数学派:
Math Pi是扎根于香港中文大学(深圳)课程、以数学学习和研究为主题的新生社团,秉着提高同学们学习数学的热情与兴趣,打造良好的校园数学学习氛围为宗旨,社团试运行期间得到了同学们的积极参与与广泛支持,关注人数赶超其他新老社团。请相信,我们能带给你的将不止这些。
目瞪口呆.jpg
哈哈哈!好棒!
哦豁?优秀(˶‾᷄ ⁻̫ ‾᷅˵)
微信内置浏览器中图片不能放大,所以路径2尼玛的到底是哪条路啊丢!
好厉害,不过四、五路径里有些人会在台阶处就斜线往上走(这么说能明白吗?
能
明白就好~(不太明白之前那个-1是什么,又不是个观点有什么可不赞同的,手动破涕为笑
点赞失败,点成了-1
茴香豆的茴字有几种写法啊?同学们
6666666 理科生也看不懂啊哈哈哈我对不起我的物理老师
什么玩意
“外国有一位博学的学者,写了一本长达数百页的专著,论证白糖在冰淇淋中的作用。这位学者使出浑身解数,又是图表,又是方程式,当然不缺少统计数字,洋洋洒洒,如悬河泻水,不由得你不信。最后的结论是:白糖在冰淇淋中的作用就是使它甜。你不能说这个结论不对,但是对了又如何呢?”
什么东西都图个有用就没意思了
知乎上有个问题,知道「地球绕着太阳转」这些事有什么用呢?有很多说理的答案,我唯独最喜欢那句「单是知道,就很开心啊。」人生有太多事是没有意义的,对宇宙而言,甚至人生也没有意义。要什么意义呢?单是知道,就很开心。
求知跟装逼是两回事吧
其实我觉得在理想化条件下,利用co2的呼出量来代表能量消耗水平,再通过大量实验收集样本的数据进行统计,其结果更具有说服力